Question

For $a > b > 0$ , consider
$D = {(x, y, z) \in ℝ^{3} : x^{2} + y^{2} + z^{2} \leq a^{2} and x^{2} + y^{2} \geq b^{2}} .$
Then, the surface area of the boundary of the solid 𝐷 is

$4 π (a + b) \sqrt{a^{2} - b^{2}}$
$4 π (a^{2} - b \sqrt{a^{2} - b^{2}})$
$4 π (a - b) \sqrt{a^{2} - b^{2}}$
$4 π (a^{2} + b \sqrt{a^{2} - b^{2}})$

Answer: $4 π (a + b) \sqrt{a^{2} - b^{2}}$

Solution :-

Let’s first understand the set D. Set D is the collection of all points who lie in intersection of the spherical region $x^{2} + y^{2} + z^{2} \leq a^{2}$ and the cylinderical reason $x^{2} + y^{2} \geq b^{2}$ in three dimensional space. Means we have to find surface area of the region given below

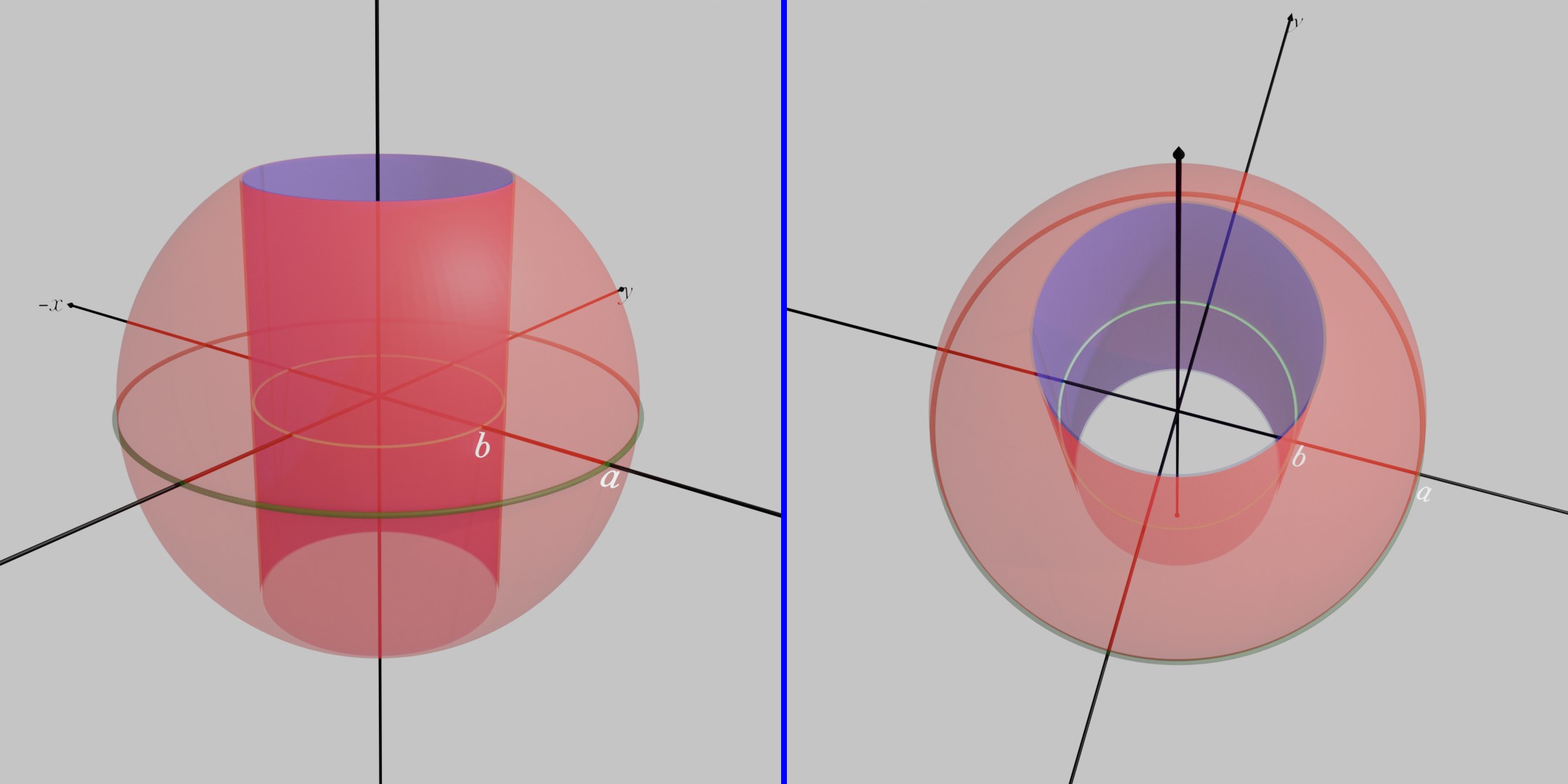
figure for set D : the surface area we have to find

Now, if we take equal sign in $x^{2} + y^{2} + z^{2} \leq a^{2} i . e ., x^{2} + y^{2} + z^{2} = a^{2}$ and intersection with $x^{2} + y^{2} \geq b^{2}$ , we get the surface area given below

Sphere Except Cylinder that lies inside the sphere

\begin{array}{rrcl} Now, & x^{2} + y^{2} + z^{2} & = & a^{2} \\ ⟹ & z^{2} & = & a^{2} - (x^{2} + y^{2}) \\ ∴ & z & = & \pm \sqrt{a^{2} - (x^{2} + y^{2})} \end{array}

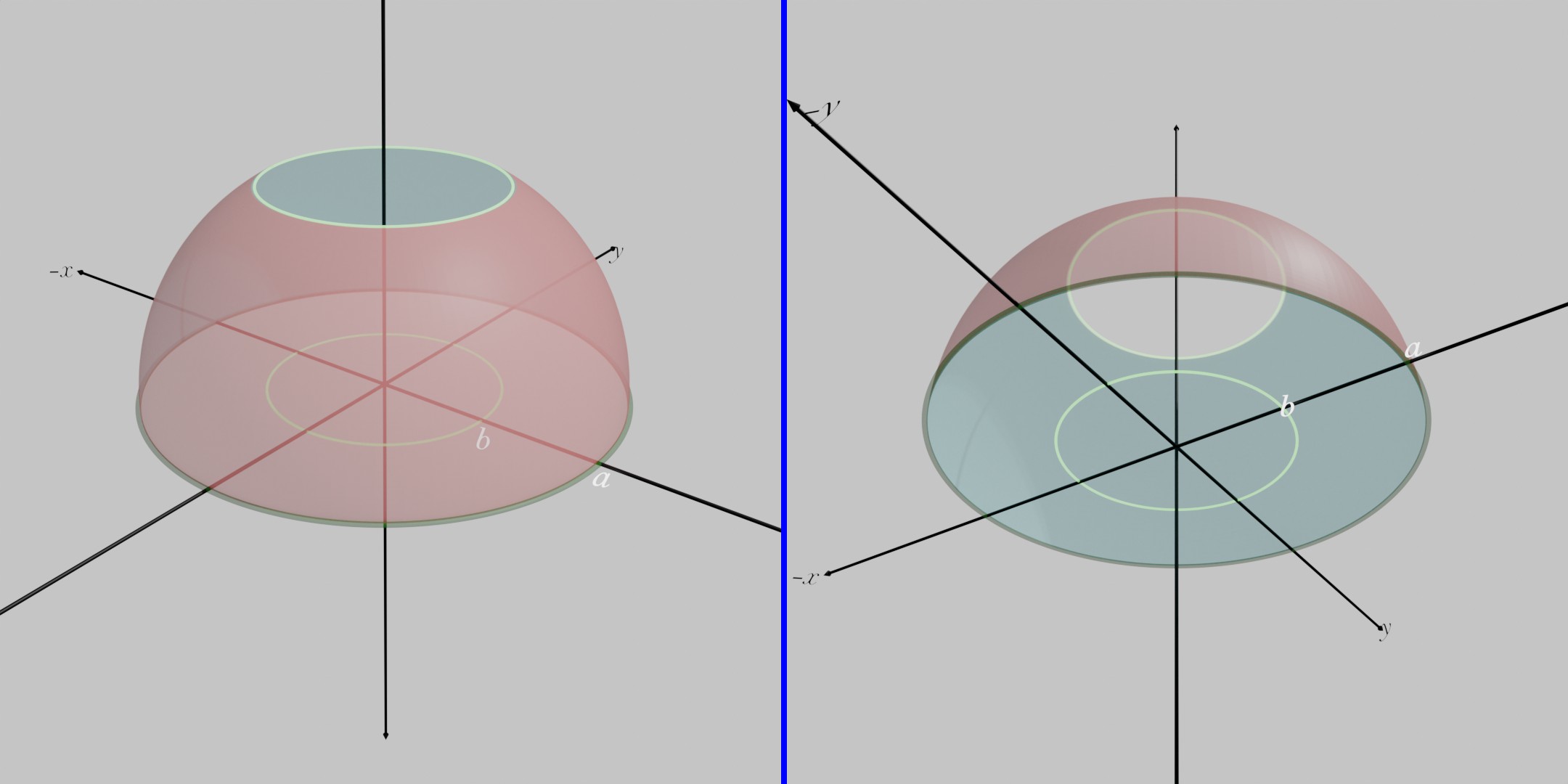
Here, if we take + sign i.e., $z = \sqrt{a^{2} - (x^{2} + y^{2})}$ and intersection with $x^{2} + y^{2} \geq b^{2}$ , we get the surface area given below

Sphere above xy-plane intersection with Cylinder

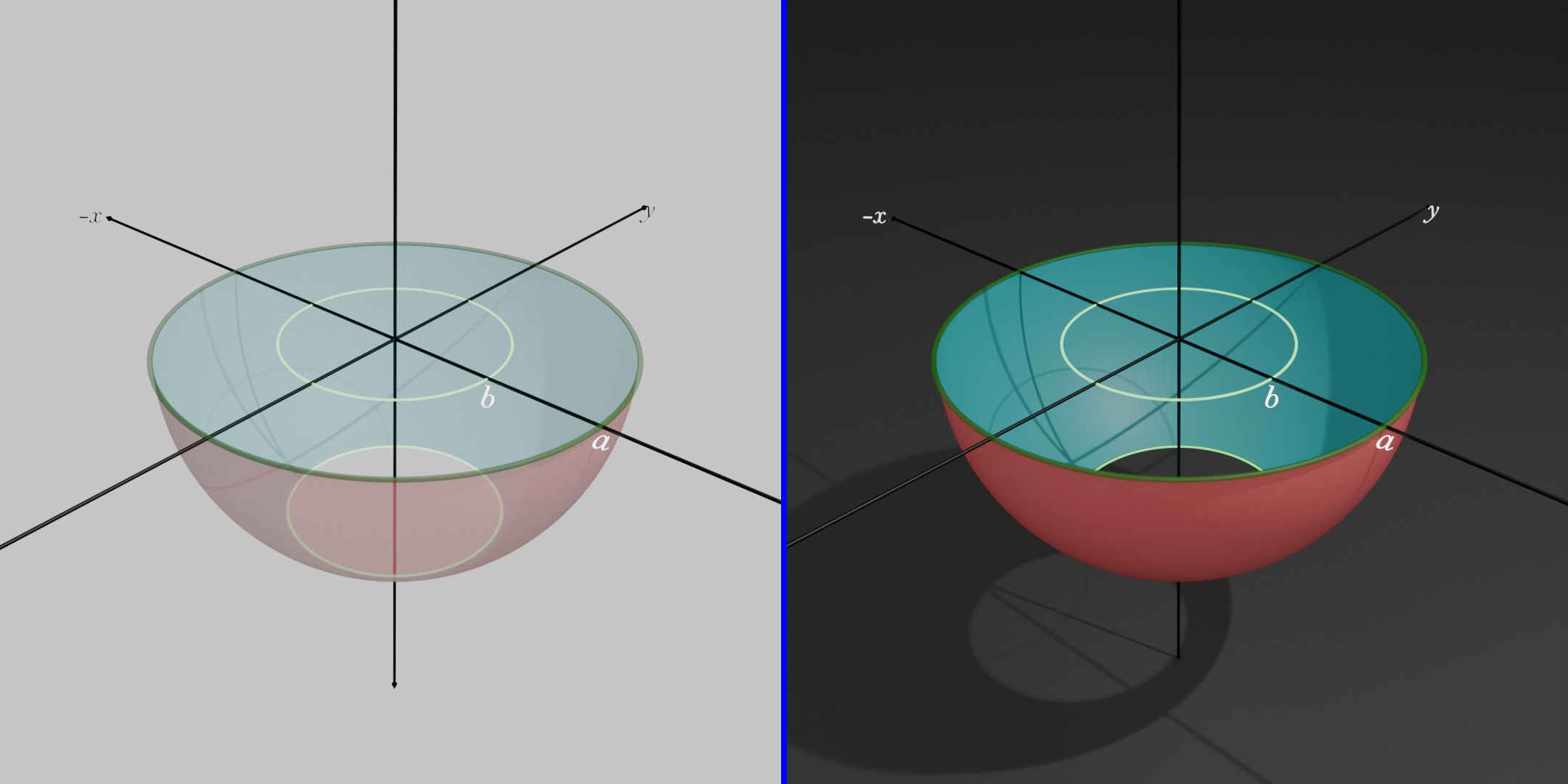
And, if we take - sign i.e., $z = - \sqrt{a^{2} - (x^{2} + y^{2})}$ and intersection with $x^{2} + y^{2} \geq b^{2}$ , we get the surface area given below

Sphere below xy-plane intersection with Cylinder

Therefore, if we want to find the surface area of the boundary of the solid 𝐷, first (i) we calculate the surface area of sphere intersection with cylinder above the xy-plane and (ii) then twice the area for below the xy-plane and (iii) add the surface area of cylinder who lie inside the sphere, we get the total surface area of the boundary of the solid 𝐷.

(i) we have to find the surface area of sphere intersection with cylinder above the xy-plane for that we take

z = \sqrt{a^{2} - (x^{2} + y^{2})}

\begin{array}{rcl} z_{x} & = & \frac{- 2 x}{2 \sqrt{a^{2} - (x^{2} + y^{2})}} = \frac{- x}{\sqrt{a^{2} - (x^{2} + y^{2})}} \\ and z_{y} & = & \frac{- 2 y}{2 \sqrt{a^{2} - (x^{2} + y^{2})}} = \frac{- y}{\sqrt{a^{2} - (x^{2} + y^{2})}} \end{array}

Now, the surface area is $S . A . = \iint_{R} \sqrt{1 + {(z_{x})}^{2} + {(z_{y})}^{2}} d A$ , where $R$ is the region of projection on xy-plane.

\begin{array}{rcl} ∴ S . A . & = & \iint_{R} \sqrt{1 + {(z_{x})}^{2} + {(z_{y})}^{2}} d A \\ = & \iint_{R} \sqrt{1 + {(\frac{- x}{\sqrt{a^{2} - (x^{2} + y^{2})}})}^{2} + {(\frac{- y}{\sqrt{a^{2} - (x^{2} + y^{2})}})}^{2}} d A \\ = & \iint_{R} \sqrt{1 + \frac{x^{2}}{a^{2} - (x^{2} + y^{2})} + \frac{y^{2}}{a^{2} - (x^{2} + y^{2})}} d A \\ = & \iint_{R} \sqrt{\frac{a^{2} - (x^{2} + y^{2}) + x^{2} + y^{2}}{a^{2} - (x^{2} + y^{2})}} d A \\ = & \iint_{R} \frac{a}{\sqrt{a^{2} - (x^{2} + y^{2})}} d A \end{array}

Projection on xy-plane :

Now, Switching to polar coordinates $(x = r cos θ, y = r sin θ)$ , we get:

\begin{array}{rcl} S . A . & = & \int_{0}^{2 π} \int_{b}^{a} \frac{a}{\sqrt{a^{2} - r^{2}}} r d r d θ \\ = & 2 π a \int_{b}^{a} \frac{1}{\sqrt{a^{2} - r^{2}}} r d r \\ = & 2 π a (2 \cdot \frac{- 1}{2}) {[\sqrt{a^{2} - r^{2}}]}_{b}^{a} \\ = & - 2 π a [- \sqrt{a^{2} - b^{2}}] \\ = & 2 π a \sqrt{a^{2} - b^{2}} . \end{array}

This is the surface area of the sphere $z = a^{2} - (x^{2} + y^{2})$ intersection with the cylinder $x^{2} + y^{2} \geq b^{2}$ above the xy-plane. (ii) Now, if we twice this surface area then we get the area above and below the xy-plane.

∴ S . A . = 2 \cdot (2 π a \sqrt{a^{2} - b^{2}}) = 4 π a \sqrt{a^{2} - b^{2}} .

(iii) Now, we have to find the surface area of cylinder $x^{2} + y^{2} \geq b^{2}$ , inside the sphere $x^{2} + y^{2} + z^{2} \leq a^{2} .$

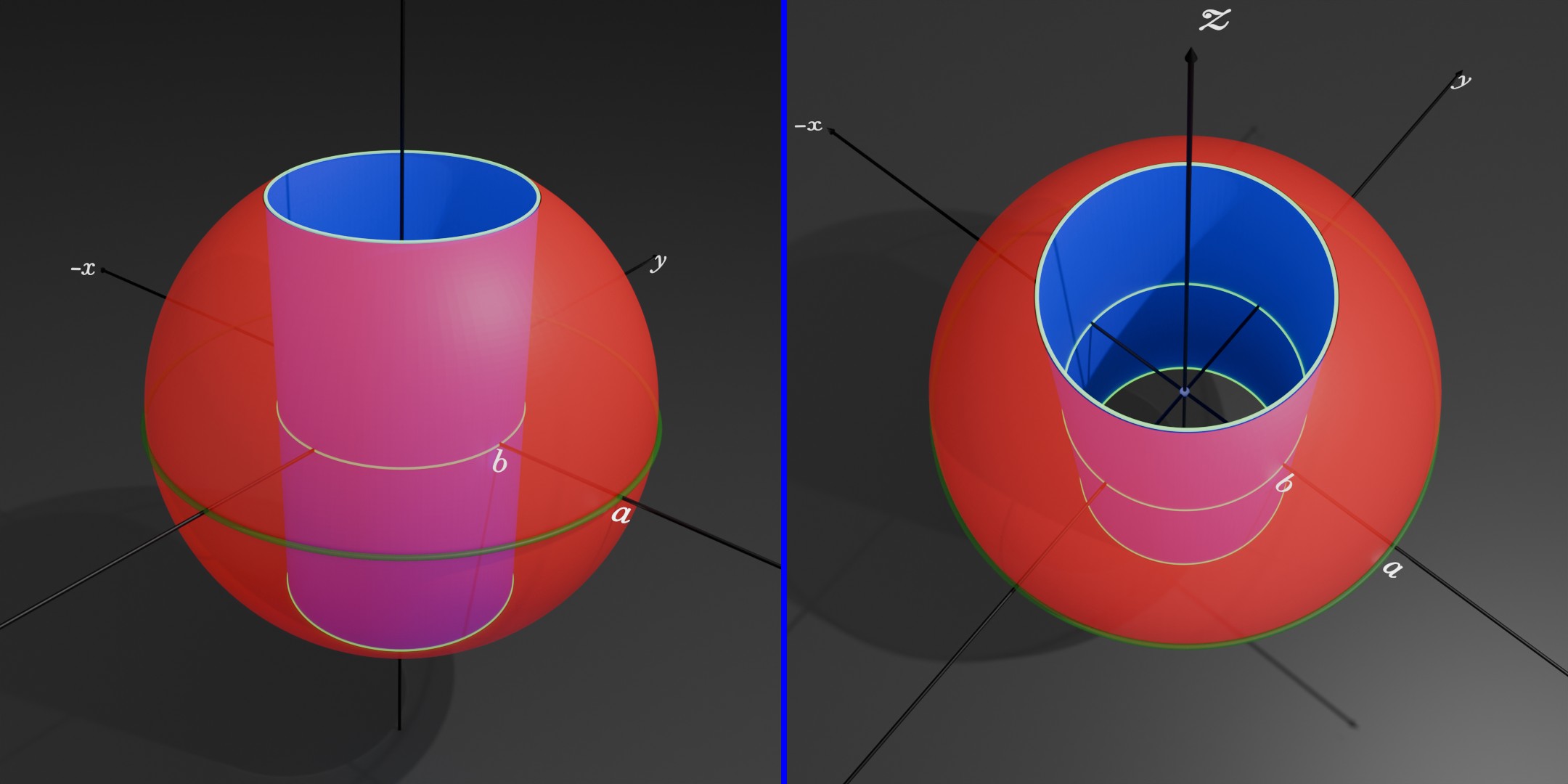
We know that the surface area of the cylinder without the top and bottom, above the xy-plane is $2 π \cdot r \cdot h .$ Here, $r = b$ and $h = \sqrt{a^{2} - b^{2}}$ (why see below)

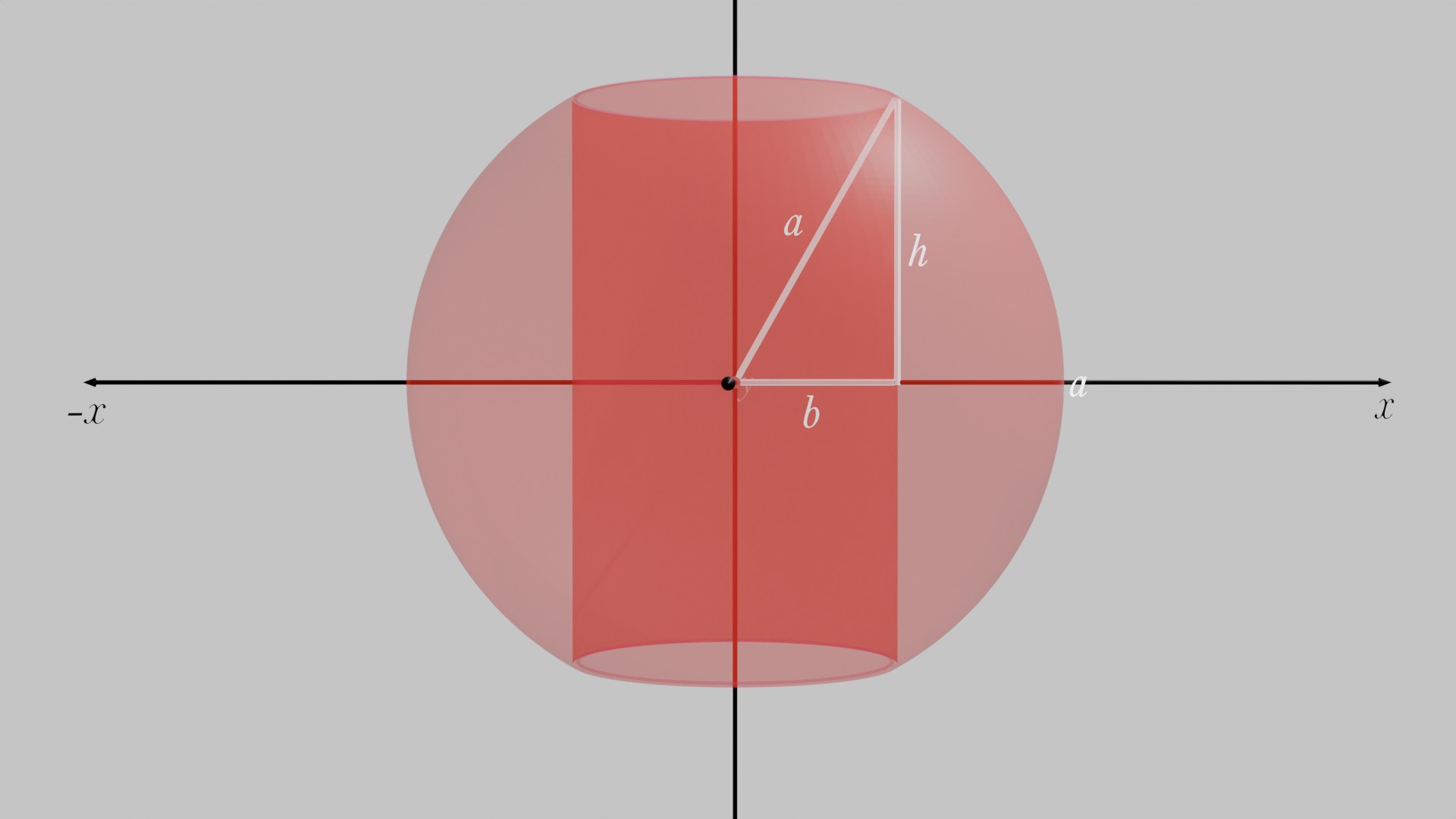
By pythagoras theorem:

\begin{array}{rrcl} a^{2} & = & h^{2} + b^{2} \\ ⟹ & h^{2} & = & a^{2} - b^{2} \\ ∴ & h & = & \sqrt{a^{2} - b^{2}} . \end{array}

Hence, the surface area of the cylinder inside the sphere above and below the xy-plane = $2 \cdot (2 π b \sqrt{a^{2} - b^{2}}) = 4 π b \sqrt{a^{2} - b^{2}} .$

Therefore, the total surface area of the boundary of the solid D is

\begin{array}{rcl} 𝐷 & = & (\begin{array}{llllllllll} surface area of sphare \\ except cylinder \end{array}) + (\begin{array}{llllllllll} surface area of cylinder \\ that lies inside the sphare \\ except sphere \end{array}) \\ 𝐷 & = & 4 π a \sqrt{a^{2} - b^{2}} + 4 π b \sqrt{a^{2} - b^{2}} \\ ∴ 𝐷 & = & 4 π (a + b) \sqrt{a^{2} - b^{2}} . \end{array}

So, the correct answer is option-1. $\to$ $4 π (a + b) \sqrt{a^{2} - b^{2}}$

#Integral Calculus #IIT JAM PYQ 2024 #Mathematics #IIT JAM PYQs

Question

For a>b>0 , consider D={(x,y,z)∈ℝ3:x2+y2+z2≤a2andx2+y2≥b2}. Then, the surface area of the boundary of the solid 𝐷 is

Solution :-

For $a > b > 0$ , consider
$D = {(x, y, z) \in ℝ^{3} : x^{2} + y^{2} + z^{2} \leq a^{2} and x^{2} + y^{2} \geq b^{2}} .$
Then, the surface area of the boundary of the solid 𝐷 is